Dicas de Matemática
Cálculo de Área
Imagine a seguinte situação:
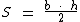
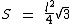
 A medida da base de um triângulo é de 7 cm, visto que a medida da sua altura é de 3,5 cm, qual é a área deste triângulo?
A medida da base de um triângulo é de 7 cm, visto que a medida da sua altura é de 3,5 cm, qual é a área deste triângulo?
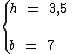
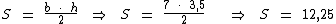
 A área deste triângulo é 12,25 cm2.
A área deste triângulo é 12,25 cm2.
 Os lados de um triângulo equilátero medem 5 mm. Qual é a área deste triângulo equilátero?
Os lados de um triângulo equilátero medem 5 mm. Qual é a área deste triângulo equilátero?
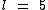
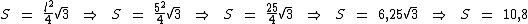
 A área deste triângulo equilátero é de aproximadamente 10,8 mm2.
A área deste triângulo equilátero é de aproximadamente 10,8 mm2.
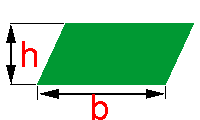

 A medida da base de um paralelogramo é de 5,2 dm, sendo que a medida da altura é de 1,5 dm. Qual é a área deste polígono?
A medida da base de um paralelogramo é de 5,2 dm, sendo que a medida da altura é de 1,5 dm. Qual é a área deste polígono?
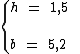
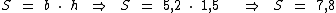
 A área deste polígono é 7,8 dm2.
A área deste polígono é 7,8 dm2.
 Qual é a medida da área de um paralelogramo cujas medidas da altura e da base são respectivamente 10 cm e 2 dm?
Qual é a medida da área de um paralelogramo cujas medidas da altura e da base são respectivamente 10 cm e 2 dm?
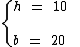
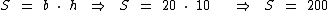
 A medida da área deste paralelogramo é 200 cm2 ou 2 dm2.
A medida da área deste paralelogramo é 200 cm2 ou 2 dm2.
Imagine a seguinte situação:
Área é a denominação dada à medida de uma superfície. Na situação acima estamos nos referindo às áreas da sala e do ladrilho.
Partindo-se deste princípio, o nosso problema se resume ao cálculo da razão entre as áreas da sala e do ladrilho.
Para que você saiba solucionar, dentre outros, o problema acima,
vamos então nos atentar ao método de cálculo da área das figuras
geométricas planas mais comuns.
Cálculo da Área do Triângulo

Denominamos de triângulo a um polígono de três lados.
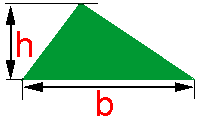
Observe a figura ao lado. A letra h representa a medida da altura do triângulo, assim como letra b representa a medida da sua base.
A área do triângulo será metade do produto do valor da medida da
base, pelo valor da medida da altura, tal como na fórmula abaixo:
A letra S representa a área ou superfície do triângulo.

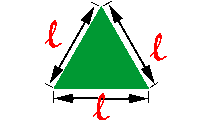
No caso do triângulo equilátero, que possui os três ângulos internos
iguais, assim como os seus três lados, podemos utilizar a seguinte
fórmula:
Onde l representa a medida dos lados do triângulo.
Exemplos
 A medida da base de um triângulo é de 7 cm, visto que a medida da sua altura é de 3,5 cm, qual é a área deste triângulo?
A medida da base de um triângulo é de 7 cm, visto que a medida da sua altura é de 3,5 cm, qual é a área deste triângulo?
Do enunciado temos:
Utilizando a fórmula:
 A área deste triângulo é 12,25 cm2.
A área deste triângulo é 12,25 cm2. Os lados de um triângulo equilátero medem 5 mm. Qual é a área deste triângulo equilátero?
Os lados de um triângulo equilátero medem 5 mm. Qual é a área deste triângulo equilátero?
Segundo o enunciado temos:
Substituindo na fórmula:
 A área deste triângulo equilátero é de aproximadamente 10,8 mm2.
A área deste triângulo equilátero é de aproximadamente 10,8 mm2.Cálculo da Área do Paralelogramo

Um quadrilátero cujos lados opostos são iguais e paralelos é denominado paralelogramo.
Com h representando a medida da sua altura e com b representando a medida da sua base, a área do paralelogramo pode ser obtida multiplicando-se b por h, tal como na fórmula abaixo:
Exemplos
 A medida da base de um paralelogramo é de 5,2 dm, sendo que a medida da altura é de 1,5 dm. Qual é a área deste polígono?
A medida da base de um paralelogramo é de 5,2 dm, sendo que a medida da altura é de 1,5 dm. Qual é a área deste polígono?
Segundo o enunciado temos:
Substituindo na fórmula:
 A área deste polígono é 7,8 dm2.
A área deste polígono é 7,8 dm2. Qual é a medida da área de um paralelogramo cujas medidas da altura e da base são respectivamente 10 cm e 2 dm?
Qual é a medida da área de um paralelogramo cujas medidas da altura e da base são respectivamente 10 cm e 2 dm?
Sabemos que 2 dm equivalem a 20 cm, temos:
Substituindo na fórmula:
 A medida da área deste paralelogramo é 200 cm2 ou 2 dm2.
A medida da área deste paralelogramo é 200 cm2 ou 2 dm2.
Comentários
Postar um comentário